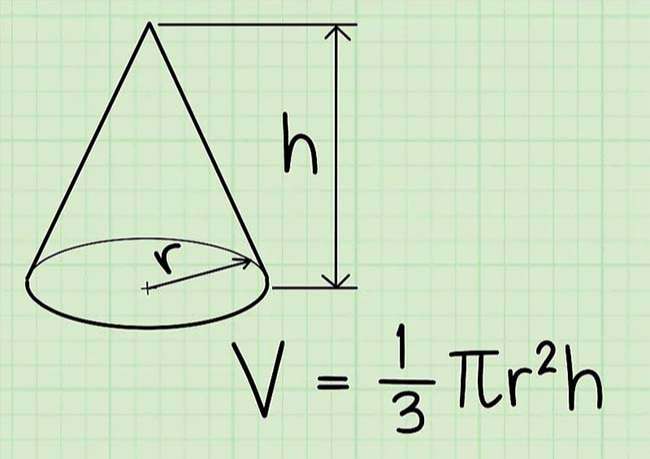Công thức tính thể tích khối nón V = (π * r^2 * h) / 3 sẽ giúp mọi người tính toán nhanh chóng và chính xác. Ngoài ra, các công thức tính thể tích khối nón tròn xoay, khối nón cụt, khối nón có đường sinh,… cũng được tổng hợp trong bài viết này của Ngân Hàng AZ.

Hình khối nón là hình gì?

Hình khối nón là một hình học không gian có một mặt phẳng và một mặt cong, đỉnh và đáy. Nó được tạo ra bằng cách quay một tam giác vuông quanh một góc vuông cố định. Nó được sử dụng trong nhiều mục đích như trang phục, trang sức hoặc biểu tượng của một tổ chức hoặc đảng phái. Có nhiều loại hình khối nón khác nhau, trong đó hình phổ biến nhất là:

• Hình nón tròn xoay: Là hình nón có đỉnh nối vuông góc với mặt đáy tâm hình tròn.
• Hình nón cụt: Là hình nón có 2 hình tròn song song nhau.
• Hình nón xiên: Là hình nón có đỉnh không kéo vuông góc với tâm hình tròn mà có thể kéo từ 1 điểm bất kỳ mà không phải tâm của hình tròn mặt đáy.

Công thức tính thể tích khối nón

Tính thể tích khối nón

Công thức tính thể tích của hình nón là:

V = (π * r^2 * h) / 3

Trong đó:

V là thể tích của hình nón

r là bán kính của mép tròn

h là chiều cao của hình nón

π (pi) là số pi = 3.14.

Tính thể tích khối nón tròn xoay

Công thức tính thể tích của khối nón tròn xoay là:

V = (π * r^2 * h) / 3

Trong đó:

V là thể tích của hình nón

r là bán kính của mép tròn

h là chiều cao của hình nón

π (pi) là số pi = 3.14.

Ví dụ: Giả sử bán kính đáy hình nón là 4cm và chiều cao của hình nón là 5cm. Thể tích của hình nón cụt là: V = (π/3) x (4cm)^2 x (5cm) = (π/3) x 16 x 5 = (4π/3) x 5 = 20π cm^3.

Tính thể tích khối nón cụt

Thể tích của khối nón cụt có thể tính bằng công thức sau:

V = πh(R^2 + r^2) / 2

trong đó:

V là thể tích của khối nón cụt

π là số pi (khoảng 3.14)

h là chiều cao của khối nón cụt

R và r là bán kính của hai hình tròn mặt đáy song song nhau

Tính thể tích khối nón đường sinh

Thể tích khối nón đường sinh được tính dựa trên công thức: V = (π * r^2 * h) / 3, trong đó:

V là thể tích khối

π là số pi, khoảng 3.14

r là bán kính nửa tròn cắt của nón đường sinh

h là chiều cao của nón đường sinh.

Thể tích khối cầu ngoại tiếp hình nón

Công thức tính thể tích khối cầu ngoại tiếp hình nón là: V = (1/3)πr^2h, trong đó r là bán kính của nón và h là chiều cao của nón.

Tính thể tích khối nón có bán kính và đường sinh

Để tính thể tích của một cầu ngoại tiếp hình nón có bán kính và đường sinh, bạn cần tìm ra hình dạng của nón. Nếu nón là một hình nón đơn giản với bán kính r và chiều cao h, thì thể tích của nón có thể tính bằng công thức: V = (1/3)πr^2h.

Nếu nón có đường sinh, bạn cần tìm ra công thức của đường sinh và sử dụng phép tích vòng tròn để tính thể tích của nón. Công thức tổng quát cho phép tích vòng tròn là: V = ∫πr^2dh, trong đó r là bán kính của đường sinh tại mỗi điểm chiều cao h. Bạn cần áp dụng công thức này với công thức của đường sinh để tìm ra thể tích của nón.

Các công thức tính toán hình nón

• Tính thể tích hình nón cầu: Tính thể tích hình nón cầu dựa trên công thức V = (1/3)πr^2h, trong đó r là bán kính của đáy hình nón và h là chiều cao của hình nón.
• Tính diện tích bề mặt hình nón: Tính diện tích bề mặt hình nón dựa trên công thức A = 2πrh + πr^2, trong đó r là bán kính của đáy hình nón và h là chiều cao của hình nón.
• Tính chiều cao hình nón dựa vào thể tích: Tính chiều cao hình nón dựa vào thể tích dựa trên công thức V = (1/3)πr^2h, r là bán kính của đáy hình nón và V là thể tích của hình nón.
• Tính bán kính hình nón dựa vào thể tích: Tính bán kính hình nón dựa vào thể tích dựa trên công thức V = (1/3)πr^2h, h là chiều cao của hình nón và V là thể tích của hình nón.

Cách xác định đường sinh, đường cao, và bán kính đáy của hình nón

Đường sinh của hình nón là một đường cong trong hình nón mà bạn có thể dựa vào để tính thể tích hoặc diện tích bề mặt. Trong toán học, đường sinh của hình nón được xác định bởi hai điểm trên đường sinh và một điểm trên mép của hình nón. Có một số cách để tìm ra bán kính đường tròn đáy của hình nón, trong đó có:

• Sử dụng công thức diện tích hình nón: V = π * r^2 * h / 3, trong đó r là bán kính đường tròn đáy, h là chiều cao của nón.
• Sử dụng công thức diện tích hình tròn: S = π * r^2, trong đó S là diện tích đáy của nón.
• Sử dụng hình dạng của đường sinh: Đường sinh của hình nón có dạng hình parabol, với độ lệch của đường sinh bằng nửa chiều cao của nón. Chọn một trong các phương pháp trên và sử dụng các giá trị của chiều cao và diện tích đáy của nón để tìm ra bán kính đường tròn đáy và sau đó tính ra đường sinh của nón.

Cách xác định đường cao của hình nón: Đường cao của một hình nón là đường thẳng kết nối giữa trung điểm của đường tròn đáy và điểm trên đỉnh của hình nón.

Cách xác định bán kính đáy của hình nón: Bán kính đáy của một hình nón có thể được xác định bằng cách tính khoảng cách giữa trung điểm của đường tròn đáy và bất kỳ điểm nào trên đường tròn đáy. Hoặc cũng có thể xác định bằng cách sử dụng công thức diện tích của hình nón và chiều cao của nó.

Các bài tập tính thể tích khối nón có lời giải

Theo DapAnChuan cho 1 số bài tập ví dụ sau: 

Bài 1: Cho hình nón có chiều cao là 3a, bán kính đáy là 4a. Tính đường sinh, diện tích xung quanh, diện tích toàn phần và thể tích của hình nón trên.

Để giải bài toán, ta có:

Đường sinh: Đường sinh của hình nón là đường nối tâm đáy đến trục cao nhất của hình nón. Đường sinh của hình nón có chiều dài là √(4a^2 + 3a^2) = √(25a^2).

Diện tích xung quanh: Diện tích xung quanh hình nón là tổng của diện tích của một vòng tròn và một hình tròn. Diện tích xung quanh của hình nón là A = 2πr (r = 4a) + πr^2 = 2π(4a) + π(4a^2) = 28πa^2.

Diện tích toàn phần: Diện tích toàn phần của hình nón là tổng của diện tích của một vòng tròn và một hình trụ. Diện tích toàn phần của hình nón là πr^2 + πr^2h = π(4a^2) + π(4a^2)(3a) = 52πa^2.

Thể tích: Thể tích của hình nón là V = (1/3)πr^2h = (1/3)π(4a^2)(3a) = 16π

Bài 2: Cho hình nón có đường sinh l, góc tạo bởi đường sinh và mặt phẳng đáy là 30º. Tính diện tích xung quanh của hình nón đó.

Để tính diện tích xung quanh của hình nón, ta cần tính độ dài quanh viền và chiều cao của nón.

Với góc giữa đường sinh và mặt phẳng đáy là 30º, ta có thể sử dụng công thức sử dụng hình tam giác:

h = l * sin(30º)

Sau đó, diện tích xung quanh của hình nón là tổng của diện tích mặt trên và diện tích quanh viền:

A = 2 * π * l * h + 2 * π * (l/2)^2

Trong đó, (l/2)^2 là diện tích mặt trên của hình nón.

Bài 3: Một khối nón có thể tích bằng 30 π, nếu tăng bán kính khối nón đó lên 2 lần và giữ nguyên chiều cao thì thể tích của khối nón mới bằng bao nhiêu?

Giả sử chiều cao của khối nón ban đầu là h và bán kính của đáy là r. Thì thể tích của khối nón ban đầu là:

V = π * r^2 * h

Khi tăng bán kính của khối nón lên 2 lần, bán kính mới sẽ là 2r và thể tích mới sẽ là:

V’ = π * (2r)^2 * h = 4 * π * r^2 * h = 4 * V

Do thể tích ban đầu bằng 30π nên thể tích mới bằng 4 * 30π = 120π.

Bài 4: Cho một hình tam giác ABC vuông cân tại A có cạnh AB = 2a. Quay tam giác này xung quanh cạnh AB tạo thành hình nón. Tính thể tích của khối nón được tạo thành.

Khi quay tam giác ABC xung quanh cạnh AB, sẽ tạo thành một khối nón với đường sinh là cạnh AB = 2a.

Chiều cao của khối nón là chiều cao của tam giác ABC từ đỉnh A, có thể tính bằng h = √(a^2 – (a/2)^2) = a√(3)/2.

Thể tích của khối nón là tổng của diện tích xung quanh và diện tích mặt trên:

V = π * (2a)^2 * h/3 + π * (2a/2)^2 * h/2

= 2π * a^2 * h/3

= 4π * a^3 / (3√3)

Bài 5: Tính thể tích của khối nón biết thiết diện qua trục của nó là tam giác vuông cân. Tam giác này có cạnh huyền bằng 2a.

Thể tích của khối nón có thể tính bằng diện tích của một mặt cắt qua trục của nón, chia cho 2.

Diện tích mặt cắt qua trục của nón là diện tích của tam giác vuông cân tại trục của nón. Do đó, diện tích mặt cắt qua trục của nón là:

S = a^2 * √(3)/2

Vậy, thể tích của khối nón là:

V = S * 2a / 2 = a^3 * √(3)

Vậy, thể tích của khối nón biết thiết diện qua trục của nó là tam giác vuông cân có cạnh huyền bằng 2a là a^3 * √(3).

Bài 6: Tính thể tích khối nón có nón có chiều cao bằng 4 và đường sinh bằng 5

Thể tích của khối nón có chiều cao bằng 4 và đường sinh bằng 5 là:

V = π * (5/2)^2 * 4 / 3 = 10π

Vậy, thể tích của khối nón có chiều cao bằng 4 và đường sinh bằng 5 là 10π.

Bài 7: Cho thể tích khối nón bằng 4π vfa chiều cao là 3. Tính bán kính đường tròn đáy của khối nón

Thể tích của khối nón là 4π, chiều cao của nón là 3, vậy diện tích của đáy của nón là:

S = 4π / 3 = 4π / (1/3 * chiều cao)

Chúng ta có thể tìm ra bán kính đường tròn đáy của khối nón bằng cách sử dụng công thức diện tích hình tròn:

S = π * r^2

Vậy, chúng ta có thể tìm ra bán kính đường tròn đáy của khối nón bằng cách so sánh hai công thức trên:

π * r^2 = 4π / (1/3 * 3)

r^2 = 4 / (π * (1/3 * 3))

r = √(4 / (π * (1/3 * 3))) = √(4 / (π * 1)) = √(4 / π)

Vậy, bán kính đường tròn đáy của khối nón là √(4 / π).

Trên đây là các công thức tính thể tích khối nón chính xác nhất kèm với các ví dụ và lời giải chi tiết mà Ngân Hàng AZ đã tổng hợp. Hy vọng các thông tin trong bài sẽ giúp mọi người tính toán dễ dàng và nhanh chóng hơn. Cần thường xuyên ôn tập và giải các bài toán để vận dụng tốt các công thức toán học.